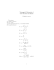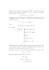Dispensa sugli studi qualitativi

0.1
Analisi qualitativa
Non sempre è possibile scrivere esplicitamente le soluzioni di un’equazione
differenziale non lineare, e del resto non sempre un’espressione esplicita aiuta
a comprendere l’andamento qualitativo delle curve integrali, ossia dei grafici
di tali soluzioni. In molti casi, uno studio diretto dell’equazione differenziale
permette di studiare il comportamento delle curve integrali senza conoscerne
l’espressione analitica.
Esempio 0.1.1 Consideriamo l’equazione del primo ordine
1
0
.
y =x 1+
y
Il teorema di esistenza e unicità della soluzione è applicabile in tutti i punti
(x, y) dei due semipiani y > 0 e y < 0: quindi per ogni punto (x0 , y0 ),
con y0 6= 0, passa una e una sola soluzione dell’equazione. Cominciamo col
determinare le curve isocline, cioè le curve sulle quali la pendenza di tutte
le curve integrali che le attraversano è la stessa. Nel nostro caso, le isocline
x
sono le iperboli di equazione y = c−x
: infatti una soluzione y(x), che passi
x0
per un punto della forma (x0 , c−x0 ), deve avere in tale punto pendenza pari
a
!
1
1
= x 0 1 + x0
y 0 (x0 ) = x0 1 +
= c,
y(x0 )
c−x0
dunque costante (al variare di tutte le soluzioni passanti per punti della
curva). In particolare, sui punti dell’isoclina y = −1 le curve integrali hanno
tangente orizzontale.
Dall’equazione differenziale ricaviamo, derivando rispetto a x,
y 00 = 1 +
(y + 1)(y − x)(y + x)
1
y0
−x 2 =
,
y
y
y3
e quindi l’intero piano può essere suddiviso in regioni di concavità e di convessità sulla base del segno dei fattori che compongono y 00 . In particolare le
rette y = ±x sono costituite da punti di flesso per le soluzioni. Si osservi che
per x < 0 e y ∈
/ [−1, 0] le soluzioni sono decrescenti, mentre sono crescenti
per y < 0 e −1 < y < 0. Inoltre le soluzioni sono apri, ossia i grafici sono
simmetrici rispetto alla retta verticale x = 0: infatti, dato che il secondo
membro dell’equazione differenziale è una funzione dispari rispetto a x, se
1
y(x) è soluzione, anche y(−x) lo è.
La retta y = −1 è una
curva integrale dell’equazione: quindi, per il teorema di unicità, essa non
può essere attraversata
da altre curve integrali.
Infine osserviamo che per
y > 0 risulta |y 0 (x)| >
|x|, e quindi |y 0 (x)| → ∞
quando x → ±∞; pertanto nessuna curva integrale presenta asintoti
obliqui.
Si noti che l’equazione differenziale, essendo a variabili separabili, si risolve,
ma la soluzione è espressa in forma implicita:
y − ln |1 + y| =
x2
+ c,
2
c ∈ R.
Esempio 0.1.2 Consideriamo l’equazione
y 0 = 4y(1 − y).
In questo caso le curve isocline sono le rette y = c; vi sono inoltre le soluzioni
costanti y = 0 e y = 1, che separano il piano in tre zone, in ciascuna delle
quali y 0 ha segno costante. Si ha anche
y 00 = 16y(1 − y)(1 − 2y),
e quindi per y > 1 e per 0 < y < 1/2 le soluzioni sono convesse.
È facile analizzare il comportamento asintotico delle soluzioni. Consideriamo
una curva integrale uscente da un punto di coordinate (0, a): se a ∈ ]0, 1[ ,
y(x) è crescente ed è contenuta nella striscia 0 < y < 1 (poiché non può
attraversare le due curve integrali y = 0 e y = 1); dal teorema di esistenza segue che y(x) esiste per ogni x ∈ R. Inoltre, posto u0 = limx→∞ y(x)
e v0 = limx→−∞ y(x) (i limiti esistono essendo y crescente), si deve avere
limx→±∞ y 0 (x) = 0, e dunque, passando al limite nell’equazione differenziale,
si trova 4u0 (1 − u0 ) = 0 = 4v0 (1 − v0 ), da cui u0 = 1 e v0 = 0. Dunque
le curve integrali costanti y = 0 e y = 1 sono asintoti orizzontali per tali
2
soluzioni.
Se invece a > 1, y(x) è convessa e decrescente, quindi u0 =
limx→∞ y(x) esiste finito e come
sopra si ottiene u0 = 1, mentre necessariamente la soluzione
diverge per x → −∞, dato che
|y 0 | ≥ 4|y|(|y| − 1) → +∞ per
x → −∞: dunque v0 = −∞.
Quando a < 0, simili considerazioni mostrano che v0 = 0 e
u0 = −∞. Si noti il diverso comportamento delle curve integrali attorno alla soluzioni stazionarie: al crescere di x, la soluzione
y = 1 è un “attrattore” di soluzioni, mentre y = 0 è un “repulsore”
di soluzioni.
In questo caso le soluzioni si determinano esplicitamente:
y(x) =
ce4x
,
1 + ce4x
c ∈ R.
Osservazione 0.1.3 L’esempio precedente rientra in una importante sottoclasse di equazioni del primo ordine: le equazioni autonome, ossia quelle della
forma
y 0 = F (y),
ove F : J → R è un’assegnata funzione continua definita su un intervallo
J ⊆ R. Dunque un’equazione differenziale è autonoma se il suo secondo
membro non dipende esplitamente dalla variabile x.
È facile verificare che se y(x) è una soluzione in ]x1 , x2 [ dell’equazione sopra
scritta, allora, qualunque sia T ∈ R, la funzione x 7→ y(x + T ) risolve l’equazione in ]x1 − T, x2 − T [ . Nel seguito supporremo per semplicità che F
sia definita su tutto R; si noti che questo non implica che ciascuna soluzione
sia definita su tutto R. È vero però che per descrivere tutte le soluzioni sarà
sufficiente, a meno di una traslazione temporale, considerare le soluzioni del
problema di Cauchy
0
y = F (y)
y(0) = y0
3
al variare di y0 in R.
Analizziamo alcuni casi significativi. Se F (y0 ) = 0, allora y(x) ≡ y0 è una
soluzione stazionaria, ossia costante. Se F (y0 ) < 0 ed esiste y < y0 tale che
F (y) = 0, allora si vede facilmente che la soluzione y(x) è definita per ogni
x > 0 e limx→+∞ y(x) = y1 , ove y1 è il massimo fra gli zeri di F minori di
y0 . Similmente, se F (y0 ) > 0 ed esiste y > y0 tale che F (y) = 0, allora la
soluzione y(x) è definita per ogni x > 0 e limx→+∞ y(x) = y2 , ove y2 è il
minimo fra gli zeri di F maggiori di y0 . Se ne deduce che se esiste un intorno
U di y0 per cui

per y < y0 , y ∈ U
 >0
per y = y0
F (y) = 0

<0
per y > y0 , y ∈ U,
allora la soluzione stazionaria y(x) = y0 è asintoto per x → +∞ di soluzioni
y(x), sia “dall’alto” che “dal basso”. Una condizione sufficiente affinché ciò
accada è, ovviamente,
F ∈ C 1 (R),
F (y0 ) = 0,
F 0 (y0 ) < 0.
Si dice in tal caso che la soluzione stazionaria y = y0 è asintoticamente stabile.
Se, invece, esiste un intorno U di y0 per cui

 < 0 per y < y0 , y ∈ U
F (y) = 0 per y = y0

> 0 per y > y0 , y ∈ U,
allora le soluzioni y(x) “si allontanano” dalla soluzione stazionaria y = y0
per x → +∞; ciò accade, ad esempio, quando F ∈ C 1 (R), F (y0 ) = 0 e
F 0 (y0 ) > 0. In tal caso la soluzione stazionaria y = y0 si dice instabile.
Discuteremo adesso alcuni esempi, che mettono in evidenza come l’analisi
della situazione, benché concettualmente non difficile, si riveli talvolta assai
complicata.
Esempio 0.1.4 Consideriamo l’equazione differenziale
y 0 = y 2 − arctan2 x.
Osserviamo anzitutto che il secondo membro verifica le ipotesi del teorema di
esistenza ed unicità su tutto R2 : quindi per ogni punto del piano passa una
4
ed una sola traiettoria. Dunque i grafici di due soluzioni distinte non possono
intersecarsi. Inoltre, se y(x) è soluzione, allora anche v(x) = −y(−x) è soluzione: ciò significa che i grafici sono simmetrici rispetto all’origine e pertanto
è sufficiente analizzarli nel semipiano x ≥ 0. Le soluzioni sono crescenti nella
regione |y| > | arctan x| e decrescenti nella regione |y| < | arctan x|; dunque
i grafici attraversano y = ± arctan x con tangente orizzontale. Le regioni di
convessità sono di difficile individuazione, poiché
y 00 = 2yy 0 − 2
arctan x
arctan x
= 2y(y 2 − arctan2 x) − 2
,
2
1+x
1 + x2
e non è per niente agevole lo studio del segno di y 00 . Tuttavia possiamo notare
che
π2
< y0 < y2,
y2 −
4
quindi, detta yb la soluzione tale che y(0) = b, per confronto si ha z(x) <
yb (x) < w(x), ove w e z sono le soluzioni dei problemi di Cauchy
0
0
2
w = w2
z = z 2 − π4
w(0) = b,
z(0) = b.
Con calcoli standard si trova dunque
π1+
z(x) =
21−
b−π/2 πx
e
b+π/2
b−π/2 πx
e
b+π/2
< yb (x) <
b
= w(x)
1 − xb
∀x > 0.
È immediato constatare che
w(x) → +∞ per x →
1
,
b
z(x) → +∞ per x →
1 b + π/2
ln
,
π b − π/2
e dunque anche yb ha un asintoto verticale x = xb , con
1
1 b + π/2
< xb < ln
;
b
π b − π/2
in particolare, se b → ∞ l’ascissa dell’asintoto di yb tende a 0.
Più in generale, se b > 0 ed esiste ξ > 0 tale che yb (ξ) = π/2, allora sarà
z(x) < yb (x) < w(x), ove w e z sono le soluzioni dei problemi di Cauchy
0
0
2
w = w2
z = z 2 − π4
w(ε + ξ) = yb (ε + ξ),
z(ε + ξ) = yb (ε + ξ),
5
ove ε > 0, e si trova di conseguenza per x > ε + ξ
π 1+
z(x) =
2 1−
yb (ε+ξ)−π/2 π(x−ε−ξ)
e
yb (ε+ξ)+π/2
yb (ε+ξ)−π/2 π(x−ε−ξ)
e
yb (ε+ξ)+π/2
< yb (x) <
yb (ε + ξ)
= w(x).
1 − (x − ε − ξ)yb (ε + ξ)
Dunque, nuovamente, la yb ha un asintoto verticale x = xb con
ε+ξ+
1
1 yb (ε + ξ) + π/2
< xb < ε + ξ + ln
.
yb (ε + ξ)
π yb (ε + ξ) − π/2
Se invece b > 0 è sufficientemente piccolo, allora il grafico di yb attraversa
b
la curva y = arctan x: infatti si ha yb (x) < 1−xb
e il grafico di quest’ultima
funzione sicuramente attraversa quello di arctan x purché b sia piccolo (infatti
per x = π/4 si ha 1−bπ b < arctan π/4 = 1 purché b < 4/(4 + π)).
4
Dunque esiste il numero positivo
n
πo
.
α = inf b > 0 : ∃ξ > 0 : yb (ξ) =
2
Se allora b > α, la corrispondente soluzione cresce fino al suo asintoto verticale x = xb ; se 0 < b < α, la soluzione cresce fino ad attraversare la curva
y = arctan x, dove ha un massimo assoluto, poi inizia a decrescere, come
vedremo meglio fra poco.
Se b = α, la soluzione yα separa le soluzioni con asintoto verticale da quelle
definitivamente decrescenti: non è difficile rendersi conto che essa dovrà essere crescente (perché è un estremo inferiore di funzioni crescenti) ma restare
sotto la quota y = π/2 per definizione di α. Dunque per questa soluzione si
ha
π
arctan x < yα (x) <
∀x > 0.
2
Osserviamo adesso che se una soluzione comincia ad essere decrescente, tale
resterà per sempre: infatti per tornare a crescere dovrebbe attraversare con
pendenza nulla, venendo dall’alto, la curva y = − arctan x, che ha pendenza
negativa, e questo è impossibile. Pertanto queste soluzioni non possono che
tendere all’asintoto orizzontale y = −π/2.
Se b = 0 la soluzione parte con pendenza nulla, cosicché viene immediatamente a trovarsi nella regione di decrescenza. Quindi anch’essa decresce fino
all’asintoto orizzontale y = −π/2.
Infine, se b < 0 la soluzione cresce, fino ad attraversare la curva y = arctan x,
dopodiché ancora una volta ls soluzione decresce fino all’asintoto orizzontale
6
y = −π/2. Si noti che per ogni b < 0 la soluzione yb (x) ≡ y(x) diventa prima
o poi decrescente: infatti supponiamo per assurdo che y(x) resti crescente
e dunque sempre minore di − arctan x: possiamo confrontare y(x) con una
soluzione u(x) di dato iniziale b0 > 0 piccolo, notando che la differenza y − u
verifica
y 0 − u0 = y 2 − u2 ,
y(0) − u(0) = b − b0 < 0.
Scegliamo un’ascissa x0 sufficientemente grande in modo che u(x0 ) < 0;
dunque v = y − u verifica
π
v0
= y + u < − + max u = −K < 0
v
2
∀x > x0 .
Ne segue facilmente
|v(x)| ≤ |v(x0 )|e−K(x−x0 ) .
D’altra parte,
y(x) < −
π
< − arctan x < u(x)
2
∀x > 0,
quindi otteniamo
|v(x0 )|e−K(x−x0 ) ≥ |v(x)| = u(x) − y(x) >
π
− arctan x
2
∀x > x0 .
Ciò tuttavia è assurdo perché per x → +∞ si ha
π
1
1
− arctan x = arctan ' .
2
x
x
Possiamo ricapitolare tutto quanto detto con questo disegno approssimativo:
7
Esempio 0.1.5 Consideriamo l’equazione differenziale
√
√
y 0 = y − x.
Essa è definita per x, y ≥ 0 ma rispetta le ipotesi del teorema di esistenza
e unicità solo quando x, y > 0. Nei punti di ordinata nulla, infatti, succede
che la soluzione con dato iniziale y(x0 ) = 0 è definita al più “nel passato”,
√
ossia per 0 ≤ x < x0 , ma non “nel futuro”, poiché si ha y 0 (x0 ) = − x0 < 0
e quindi il grafico esce immediatamente dal dominio, facendo perdere significato all’equazione differenziale. Analizziamo dunque la situazione nel primo
quadrante aperto. Le soluzioni sono sempre positive; la zona di crescenza è il
settore y > x, mentra la retta y = x viene attraversata con pendenza nulla.
Calcoliamo la regione di convessità: si ha, con qualche calcolo,
√
√
( x − 1) y − x
1
1 y0
00
√ √
=
;
y =
√ −√
2
y
x
2 x y
dunque se x ≤ 1 le soluzioni sono concave, mentre se x > 1 le soluzioni sono
x2
convesse per y ≥ (√x−1)
2 := g(x) e concave per 0 < y ≤ g(x). La funzione
g(x) tende a +∞ per x → 1+ , mentre per x → +∞ si ha
√
√
x
x(2 x − 1)
√
g(x) − x = x √
−1 =
' 2 x,
2
( x − 1)
x−2 x+1
8
cosicché g(x)−x → +∞ per x → +∞. Ne segue che g ha un minimo assoluto
per x = 4, con g(4) = 16, ed ha necessariamente un flesso fra 4 e +∞.
Osserviamo adesso un fatto importante: se y(x0 ) = g(x0 ), ossia una soluzione
taglia il luogo dei flessi g, allora x0 > 1 e
√
p
p
x0
√
√
√
x0
0
− x0 = √
,
y (x0 ) = y(x0 ) − x0 = g(x0 ) − x0 = √
x0 − 1
x0 − 1
ed è facile verificare che risulta y 0 (x0 ) > g 0 (x0 ); ciò significa che y(x) diventa
convessa e non può più riattraversare la curva y = g(x) in un altro punto
x00 > x0 poiché altrimenti in tale punto dovrebbe aversi la disuguaglianza
contraria y 0 (x00 ) ≥ g 0 (x00 ). Dunque tale soluzione tende a +∞ senza asintoto
verticale. Nemmeno può essercipun asintoto
√ obliquo y = ax + b, poiché in
0
tal caso avremmo y (x) → a e y(x) − ax + b → 0 per x → ∞, mentre
l’equazione differenziale fornirebbe invece
p
√
(a − 1)x + b
+∞ se a 6= 1
0
y (x) = y(x) − x ' √
√ '
0
se a = 1.
ax + b + x
Se invece la soluzione non taglia il grafico di g, essa rimane concava e tende
a 0 in tempo finito, ossia per x → x con x opportuno. La soluzione taglia o
no il grafico di g a seconda del suo valore iniziale b: se b è molto piccolo, la
pendenza di y(x) è troppo piccola per attraversare il grafico di g.
La famiglia delle soluzioni definitivamente convesse
è chiaramente separata da
quella delle soluzioni che
restano concave, per mezzo
di una soluzione il cui dato
iniziale α è definito da
α = sup{b > 0 : yb < g} :
tale soluzione yα (x) è l’unica concava e crescente nell’intera semiretta [0, ∞[:
essa aderirà sempre più a
g(x), nel senso che yα (x) −
g(x) → 0 per x → +∞.
9
Esempio 0.1.6 Analizziamo l’equazione
2
y 0 = xy e−y .
Vi è la soluzione nulla y = 0; inoltre se y(x) è soluzione anche y(−x) e −y(x)
sono soluzioni: pertanto basta studiare cosa succede nel primo quadrante. In
questa regione tutte le soluzioni (tranne ovviamente y = 0) sono crescenti.
Troviamo la curva dei flessi: dopo qualche calcolo si ottiene
2
2
2
y 00 = e−y [y + x(1 − 2y 2 )y 0 ] = y e−y [1 + x2 e−y (1 − 2y 2 )],
da cui y 00 ≥ 0 se e solo se
1
0≤y≤ √
2
1
oppure y > √
2
La funzione
ey
2 /2
e 0≤x≤ p
.
2y 2 − 1
2
1
ey /2
,
y>√ ,
h(y) = p
2
2y 2 − 1
+
e per y → ∞; inoltre, si verifica facilmente che
tende a +∞ per y → √12
2
y ey /2 (2y 2 − 3)
h (y) =
,
(2y 2 − 1)3/2
0
e in particolare h ha l’unico punto di minimo
relativo, dunque anche di mip
3/4
nimo assoluto, per x = e√2 , dove vale 3/2.
Consideriamo una soluzione y con y(0) = b > 0: essa parte con tangente
orizzontale ed è inizialmente convessa. Inoltre essa tende a +∞ per x → ∞:
infatti non può avere un asintoto orizzontale per x → ∞, perché dall’equazione differenziale seguirebbe che y 0 (x) → +∞ per x → ∞ e ciò è assurdo.
Se y rimanesse convessa per ogni x > 0, non appena y(x) > √12 si avrebbe
2
y 0 (x) = xy e−y ≤ e−y
2 /2
y
p
,
2y 2 − 1
da cui y 0 (x) → 0 per x → ∞: ciò è impossibile, essendo y(x) convessa
e crescente. Pertanto tutte le soluzioni con b > 0 finiscono per diventare
concave. Per giunta, esse non possono pù tornare convesse: infatti in un
10
ipotetico punto (x, y) in cui il grafico di y(x) tagliasse nuovamente la curva
x = h(y) dovremmo avere
r
3
, x = h(y),
y 0 (x) ≥ (h−1 )0 (x),
y>
2
ossia
2
ey /2
x= p
,
2y 2 − 1
2
xye−y = y 0 (x) ≥ (h−1 )0 (x) =
(2y 2 − 1)3/2
1
=
;
h0 (y)
y ey2 /2 (2y 2 − 3)
ne seguirebbe via via, equivalentemente,
2
xye−y ≥
(2y 2 − 1)3/2
(2y 2 − 1)
=
,
xy(2y 2 − 3)
y ey2 /2 (2y 2 − 3)
2
x2 y 2 e−y =
2y 2 − 1
y2
≥
,
2y 2 − 1
2y 2 − 3
(2y 2 − 3)y 2 ≥ 4y 4 − 4y 2 + 1,
2y 4 − y 2 + 1 ≤ 0,
e questo è impossibile perché la quantità a primo membro è un trinomio
sempre positivo.
Notiamo infine che y(x) tende a +∞ con y 0 (x) → 0, quindi la crescenza è di
tipo logaritmico (e in particolare senza asintoti obliqui).
Esempio 0.1.7 Consideriamo infine l’equazione
y 0 = x2 − y 2 .
11
Il teorema di esistenza e unicità vale in tutto il piano. Non vi sono soluzioni
costanti; inoltre se y(x) è soluzione, anche −y(−x) lo è: quindi è sufficiente
analizzare cosa succede nel semipiano x ≥ 0. La zona di crescenza delle
soluzioni è −x ≤ y ≤ x, e ovviamente la zona di decrescenza è |y| > x. Si ha
poi
y 00 = 2x − 2yy 0 = −2yx2 + 2x + 2y 3 ;
quindi le soluzioni sono convesse nella regione descritta dalla disuguaglianza
yx2 − x − y 3 ≤ 0, e dunque, risolvendo la disequazione di secondo grado in
x ≥ 0, si ha

p
1 + 4y 4 + 1


 0≤x≤
se y > 0

2y
00
y ≥ 0 ⇐⇒
p

1 + 4y 4 − 1


 x≥
se y < 0.
2|y|
√
1+4y 4 +1
Con calcoli un po’ laboriosi si verifica che per la funzione g(y) =
,
2y
y > 0, si ha
1/4 1
3
33/4
+
g(y) ' per y → 0 , min g = g
, g(y) ' y per y → ∞,
=
y
21/4
21/2
ed in particolare, poiché risulta g(y) > y, il grafico di g è interamente contenuto nella zona di crescenza;
calcoli altrettanto laboriosi mostrano che invece
√
la funzione h(y) =
1+4y 4 −1
,
2|y|
y < 0, soddisfa
h(y) ' −2y 3 per y → 0− ,
h(y) ' −y per y → −∞,
ed in particolare, dato che h(y) < |y|, il grafico di h è interamente contenuto
nella zona di decrescenza. Notiamo anche che
p
1 − 4y 2 − 1 + 4y 4
0
p
< 0,
h0 (y) → −1 per y → −∞.
h (y) =
2
4
2y 1 + 4y
Consideriamo una soluzione y(x) con y(0) = b. Se b > 0, la soluzione è
inizialmente decrescente e convessa; dopo aver raggiunto e superato il suo
minimo, entra necessariamente (in quanto la curva dei flessi ha per asintoto
la retta y = x) nella zona di concavità, e lı̀ resta, tendendo all’infinito in
modo concavo: non può infatti tornare convessa, perché in tal caso finirebbe
12
per riattraversare la retta y = x e ciò è impossibile, non essendo nulla la sua
derivata. Però la y(x) ha l’asintoto obliquo y = x per x → ∞. Infatti, per
concavità, x − y(x) è decrescente: quindi ha limite q per x → +∞; ma allora
y(x) ha l’asintoto y = x−q e dunque y 0 (x) → 1, e dall’equazione differenziale
segue allora subito q = 0 (altrimenti y 0 (x) tenderebbe all’infinito).
Se y(0) = 0, la soluzione entra subito nella zona di crescenza, poi da convessa
diventa concava ed evolve come le soluzioni uscenti da valori b > 0.
Se y(0) = b < 0, le cose cambiano. Se |b| è sufficientemente piccolo, la soluzione deve passare da decrescente a crescente e poi da convessa a concava, per
poi evolvere come le soluzioni precedenti: infatti y 0 (x) è piccolo, mentre la
pendenza della curva x = h(y), cioè 1/h0 (y), è negativa e grande in modulo,
e quindi le due curve si intersecano.
Se invece |b| è sufficientemente grande, la y(x) sta sotto la retta y = b+y 0 (0)x,
ove |y 0 (0)| = b2 , mentre per x ≥ a la curva x = h(y) sta sopra la retta
y = h−1 (a) + (h−1 )0 (a)(x − a), che ha pendenza vicina a −1 e tocca l’asse y
in h−1 (a) − (h−1 )0 (a)a > b. Quindi y(x) resta sempre concava e tende a−∞;
b
e dunque y(x)
poiché inoltre y 0 ≤ −y 2 si vede agevolmente che y(x) ≤ 1+bx
1
ha un asintoto verticale di ascissa xb < |b| .
Vi sarà dunque una soluzione “separatrice” tra le curve yb (x) con
dato iniziale b < 0 che restano concave e le curve yb (x) con
b < 0 che sono prima concave, poi
convesse e infine nuovamente concave. Tale soluzione separatrice
avrà dato iniziale
α = sup{b < 0 : yb00 < 0 in [0, xb [ },
e sarà sempre concava, definita sull’intera semiretta [0, ∞[ ,
e si avvicinerà indefinitamente alla curva dei flessi senza
mai attraversarla, avendo dunque
l’asintoto obliquo y = −x.
13
Esercizi
1. Si verifichi che il comportamento qualitativo delle soluzioni delle equazioni
1
1
0
y = y(1 − y) y −
,
y 0 = (y 2 − 1)
2
2
è quello descritto nelle figure sottostanti.
2. Determinare il comportamento qualitativo delle soluzioni delle seguenti
equazioni:
(i) y 0 = x2 + y 2 ,
(iii) y 0 =
(v) y 0 =
x2 y 3
1+y 2
sin2 x
1+x2
(ii) y 0 =
x2 y 2
1+y 2
,
x
(iv) y 0 = |y|(1 − y) 1+x
2 ,
,
2
2
e−y ,
(iv) y 0 = x3 (e2−y − 1).
14