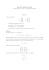Matrici ortogonali. Diagonalizzazione ortogonale per matrici

LEZIONE 25
25.1. Matrici ortogonali.
Facciamo una breve digressione su un’importante famiglia di matrici, quelle ortogonali.
Definizione 25.1.1. P ∈ Rn,n si dice ortogonale se t P P = In .
Prima di dare esempi di matrici ortogonali, facciamo alcune osservazioni.
Osservazione 25.1.2. Si noti che la matrice identità In è ortogonale in base alla definizione
data: anche ogni matrice ottenuta da In cambiando segno ad una o più delle sue entrate
è ortogonale.
Sia P ∈ Rn,n ortogonale.
i) Poiché t P P = In , segue che P è invertibile e P −1 = t P : in particolare si ha anche
P t P = In . In maniera analoga si dimostra che se P t P = In allora anche t P P = In ,
cioè P è ortogonale se e solo se P t P = In .
ii) Si ha 1 = det(In ) = det(t P P ) = det(t P ) det(P ) = det(P )2 , dunque det(P ) = ±1:
quanto sopra osservato sulla matrice identità ci permette di affermare che esistono
matrici di entrambe i tipi.
iii) Poiché la riga i–esima di t P è la colonna i–esima Pi di P , la condizione t P P = In si può
leggere dicendo che il prodotto scalare standard (si veda l’Esempio 24.1.5 con la solita
identificazione di Rn con Rn,1 ) delle colonne Pi e Pj di P è δi,j : in altre parole una
matrice è ortogonale se e solo se le sue colonne sono un insieme ortonormale, rispetto
al prodotto scalare standard, di n vettori di Rn,1 .
iv) In maniera simile, poiché anche P t P = In , anche le righe di P formano un insieme
ortonormale, rispetto al prodotto scalare standard, di n vettori di R1,n .
Le matrici ortogonali si dividono, quindi, in due classi non vuote, quelle con determinante 1 e quelle con determinante −1. Ha senso dare un nome a questi due tipi di matrici.
Definizione 25.1.3. Sia P ∈ Rn,n ortogonale. P si dice speciale se det(P ) = 1 non
speciale det(P ) = −1.
Grazie a quanto osservato sopra, siamo perciò in grado di dare esempi non banali di
matrici ortogonali.
Esempio 25.1.4. Le matrici

1
1
P1 =  2
3
2
di R3,3
2
1
−2

2
−2  ,
1


1 2 2
1
P2 =  2 1 −2  ,
3
−2 2 −1
Typeset by AMS-TEX
1
2
25.1. MATRICI ORTOGONALI
sono ortogonali. La prima è non speciale, la seconda speciale.
Esempio 25.1.5. Determiniamo tutte le matrici ortogonali d’ordine 2. Sia
p1,1 p1,2
P =
∈ R2,2
p2,1 p2,2
ortogonale. La condizione P t P = I2 si traduce allora nel sistema
 2
2

 p1,1 + p1,2 = 1
p1,1 p2,1 + p1,2 p2,2 = 0

 2
p2,1 + p22,2 = 1.
La prima e la terza equazione implicano l’esistenza di ϑ, ϕ ∈ [0, 2π] tali che p1,1 = cos ϕ,
p1,2 = − sin ϕ, p2,1 = sin ϑ, p2,2 = cos ϑ. La seconda equazione è allora equivalente a
0 = cos ϕ sin ϑ − sin ϕ cos ϑ = sin(ϑ − ϕ).
In particolare, a meno di multipli di 2π, si deve avere o ϕ = ϑ ovvero ϕ + π = ϑ. Nel
primo caso
cos ϕ − sin ϕ
P =
,
sin ϕ cos ϕ
(in tal caso P è ortogonale speciale) nel secondo
cos ϕ − sin ϕ
P =
− sin ϕ − cos ϕ
(in tal caso P è ortogonale non speciale).
Esempio 25.1.6. Si considerino nel piano due sistemi di riferimento O~ı~ e O~ı 0~ 0 . Assumiamo che O~ı 0~ 0 sia ruotato di un angolo ϕ in senso antiorario rispetto a O~ı~
y
x'
y'
v
ϕ
O
Figura 25.1.6.1
x
LEZIONE 25
3
Dato ~v = x~ı + y~ , vogliamo determinare la decomposizione ~v = x0~ı 0 + vy0 ~ 0 . Si deve
avere ~ı 0 = a~ı + b~ , ~ 0 = c~ı + d~ e si ha, per la Proposizione 24.2.6 ii),
a = h~ı 0 ,~ı i = cos ϕ,
c = h~ 0 ,~ı i = − sin ϕ,
b = h~ı 0 , ~ i = sin ϕ,
d = h~ 0 , ~ i = cos ϕ.
Se ora considero ~v = x0~ı 0 + y 0~ 0 = x~ı + y~ , sostituendo le espressioni ottenute sopra di ~ı 0
e ~ 0 in funzione di ~ı e ~ , tenendo conto che (~ı , ~ ) è una base di V2 (O), si ottiene
0 x
cos ϕ sin ϕ
x
=
.
0
y
− sin ϕ cos ϕ
y
Concludiamo che le matrici ortogonali speciali corrispondono alle rotazioni nel piano. Per
questo spesso indichiamo con Rϕ la matrice
cos ϕ sin ϕ
.
− sin ϕ cos ϕ
Un’analoga interpretazione può essere data per matrici ortogonali in Rn,n con n ≥ 3.
25.2. Diagonalizzazione ortogonale per matrici simmetriche.
Come abbiamo visto, ogni matrice A ∈ Simn (R) è diagonalizzabile (si veda la Proposizione 23.2.1). Il risultato principale di questa sezione è che la matrice che diagonalizza
può essere scelta ortogonale, quindi tale che P −1 = t P .
Infatti siano λ1 , . . . , λh ∈ R gli autovalori a due a due distinti di A. In ciascuno degli
autospazi EA (λj ) fisso una base, diciamo Bj = (Pj,1 , . . . , Pj,mj ) ove mj = ma (λj , A) =
mg (λj , A). Per la Proposizione 24.2.5 Bj può essere supposta ortonormale rispetto al
prodotto scalare standard di Rn,1 (si veda l’Esempio 24.1.5 con la solita identificazione di
Rn,1 con Rn ).
Si noti che autovettori di A relativi ad autovalori distinti sono fra loro ortogonali. Infatti,
se Pi ∈ EA (λi ) e Pj ∈ EA (λj ) con λi 6= λj , allora
λj t Pi Pj = t Pi (APj ) = t Pi APj = t Pi t APj = t (APi )Pj = λi t Pi Pj .
Quindi (λj − λi )t Pi Pj = 0: poiché λj 6= λi segue λj − λi 6= 0, dunque t Pi Pj = 0
necessariamente.
Quanto detto ci permette di affermare che è sempre possibile trovare una base ortonormale di autovettori di A, ovvero una matrice ortogonale P ∈ Rn,n tale che P −1 AP sia
diagonale. Più precisamente
Proposizione 25.2.1. Sia A ∈ Simn (R). Allora esiste una matrice ortogonale P ∈ Rn,n
tale che P −1 AP = t P AP sia diagonale. La matrice P può essere scelta speciale. Illustriamo quato detto con un esempio.
4
25.2. DIAGONALIZZAZIONE ORTOGONALE PER MATRICI SIMMETRICHE
Esempio 25.2.2. Sia

0
A = 1
1

1 1
0 1.
1 0
Come già visto nell’Esempio 23.2.2, gli autovalori di A sono −1 e 2 e
EA (−1) = L(t ( 1 −1
0),t (1
EA (2) = L(t ( 1
0 −1 )),
1
1 )).
Per ottenere una matrice ortogonale P che diagonalizzi A è necessario determinare tre
autovettori P1 , P2 , P3 ortonormali. A tale scopo basta determinare basi ortonormali in
EA (−1) e EA (2). Per quanto riguarda EA (2) basta andare a scegliere in esso un versore,
ad esempio consideriamo
 
1
1  
1 .
P1 = √
3 1
Invece il discorso è un po’ più complicato in EA (−1). Iniziamo a determinare un versore,
per esempio


1
1 
P2 = √
−1  .
2
0
Per determinare P3 cerchiamo α ∈ R tale che i vettori P2 e




1
1
Xα =  −1  + α  0 
−1
0
√
siano ortogonali. Si ha che hP2 , Xα i = (2 + α)/ 2. Affiché hP2 , Xα i = 0 si deve avere che
α = −2, dunque possiamo scegliere


−1
1
P3 = √  −1  .
6
2
Quindi la matrice ortogonale cercata è
 1
√

P =
3
√1
3
√1
3
√1
2
− √12
0

− √16
− √16 
.
√2
6
P è non speciale e risulta

2
−1
t

P AP = P AP = 0
0
0
−1
0

0
0 .
−1
LEZIONE 25
5
Per esercizio si verifichi invece che


P0 = 
√1
3
√1
3
√1
3
− √12
√1
2

− √16
− √16 

√2
6
0
è non speciale e che ancora risulta

2
P 0−1 AP 0 = t P 0 AP 0 =  0
0
0
−1
0

0
0 .
−1