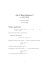TEOREMI DI ESISTENZA E UNICIT`A. Sia dato un problema di
Transcript
TEOREMI DI ESISTENZA E UNICITÀ. Sia dato un problema di Cauchy del primo ordine ẏ = f (t, y) y(t0 ) = y0 (1) La funzione f è definita in I × D, dove I è un intervallo che contiene t0 al suo interno, e D è un intervallo che contiene y0 al suo interno. Definizione. Una funzione ϕ(t) definita su un intervallo J = (t0 −a, t0 +b) ⊆ I (a, b > 0) è una soluzione di (1) definita su J se ϕ0 (t) = f (t, ϕ(t)), ϕ(t0 ) = y0 . ∀t ∈ J Attenzione! Quando si parla di soluzione di un problema di Cauchy si intende una funzione definita su un intervallo J che contiene l’istante iniziale t0 . Anche se la funzione risulta definita su altri intervalli (disgiunti da J), essa è soluzione del problema di Cauchy solo sull’intervallo J. Teorema di esistenza locale delle soluzioni (Peano). Sia dato il problema di Cauchy ẏ = f (t, y) y(t0 ) = y0 dove f (t, y) è continua su I × D. Allora ∃δ > 0 ed esiste una soluzione del problema di Cauchy, cioè una funzione ϕ(t) definita e derivabile su [t0 − δ, t0 + δ] ⊆ I tale che: ϕ0 (t) = f (t, ϕ(t)), ϕ(t0 ) = y0 . ∀t ∈ [t0 − δ, t0 + δ] (2) Osservazioni. 1. Quando si dice che una funzione è derivabile su un intervallo chiuso [a, b], si intende che è definita su un intervallo più grande [a − ε, b + ε], ed è derivabile in tutti i punti dell’intervallo [a, b] in esso contenuto. 2. La soluzione cosı̀ trovata è necessariamente derivabile con continuità su [t0 − δ, t0 + δ] perché dalla (2) si vede che ϕ0 è continua, in quanto composizione di funzioni continue. 3. Il teorema ci garantisce che localmente, vicino all’istante iniziale t0 , esiste una soluzione. Non ci assicura né che la soluzione esista su intervalli più grandi, né che sia l’unica soluzione passante per il punto (t0 , y0 ) assegnato. Il seguente esempio ci mostra che se f è soltanto continua ci può essere più di una soluzione. 1 Esempio. Sia dato il problema di Cauchy √ ẏ = 3 y y(0) = 0 (3) √ La funzione f (t, y) = 3 y è continua su tutto R. Si osserva subito che la funzione ϕ(t) = 0, r ∀t ∈ R è una soluzione di (3). Si vede però che anche le 3 funzioni g1,2 (t) = ± 23 t sono soluzioni per tutte le t ≥ 0. Poiché g1,2 hanno derivata destra nell’origine uguale a 0, risulta che il problema di Cauchy (3) ha almeno le 3 soluzioni: t≥0 0, r 3 ϕ1 (t) = 2 t , t>0 3 ϕ2 (t) = t≤0 0,r − , 3 2 t 3 , t>0 ϕ3 (t) = 0, ∀t ∈ R. Il seguente teorema ci dà delle condizioni sotto le quali l’unicità locale delle soluzioni è garantita. Teorema di esistenza e unicità locale delle soluzioni (di Cauchy). ẏ = f (t, y) y(t0 ) = y0 dove f (t, y) è continua su I × D, e ∂f (t, y) è continua in un intorno di (t0 , y0 ). ∂y Allora ∃δ > 0, e esiste una soluzione del problema di Cauchy, cioè una funzione ϕ(t) definita e derivabile su [t0 − δ, t0 + δ] ⊆ I tale che: ϕ0 (t) = f (t, ϕ(t)), ϕ(t0 ) = y0 . ∀t ∈ [t0 − δ, t0 + δ] (4) La funzione ϕ(t) è l’unica soluzione che passa per (t0 , y0 ), nel senso che ogni altra soluzione che passa per quel punto coincide con ϕ(t) su tutto l’intervallo [t0 − δ, t0 + δ]. Ci si può chiedere cosa accade se nell’estremo t0 + δ dell’intervallo di definizione di ϕ sono ancora verificate le ipotesi del teorema di esistenza e unicità, dunque se per (t0 + δ, ϕ(t0 + δ)) passa un’unica soluzione ψ(t). Per quanto detto prima, ϕ e ψ coincidono per tutte le t ≤ t0 + δ su cui entrambe le funzioni sono definite. In questo modo si ottiene un prolungamento della soluzione su un intervallo più grande del precedente. Possiamo essere sicuri che questo procedimento abbia fine solo quando si arriva all’estremo t0 + a dell’intervallo dei tempi su cui f è continua? La risposta in generale è negativa. Si dimostra un teorema che ci dice che se su tutti i punti del dominio di f sono soddisfatte le ipotesi del teorema di esistenza e unicità, per 2 ogni soluzione esiste un intervallo aperto (α, β) oltre il quale non è possibile definire la soluzione stessa. Questo intervallo è detto intervallo massimale di definizione della soluzione considerata. Si dimostra inoltre che, quando t → β, la soluzione tende all’infinito (si dice che va all’infinito in tempo finito) oppure si avvicina sempre più alla frontiera del dominio di f . Si possono dare condizioni su f sotto le quali si ha la garanzia che tutte le soluzioni sono globali, cioè sono definite su tutto l’intervallo dei tempi su cui f è definita. I teoremi sopra enunciati si estendono anche al caso di equazioni di ordine qualsiasi. In questo caso il problema di Cauchy prende la seguente forma: (n) y = f (t, y, y 0 , . . . , y (n−1) ) y(t0 ) = y0 y 0 (t0 ) = y1 .. . (n−1) y (5) (t0 ) = yn−1 In questo caso la funzione f è una funzione di n + 1 variabili, il tempo t e altre n variabili reali (x0 , . . . , xn−1 ), che per noi sono poi x1 = y, x2 = y 0 , . . . , xn = y (n−1) . f deve essere definita se t varia in un intervallo I che contiene t0 al suo interno, e le altre variabili variano in un insieme aperto D che contiene (y0 , . . . , yn−1 ) al suo interno. Teorema di Peano per le equazioni di ordine n. Sia dato il problema di Cauchy (5), con f continua in I × D. Allora ∃δ > 0 ed esiste una soluzione del problema di Cauchy, cioè una funzione ϕ(t) definita e derivabile n volte su [t0 − δ, t0 + δ] ⊆ I tale che: (n) = f (t, ϕ, ϕ0 , . . . , ϕ(n−1) ), ϕ ϕ(t0 ) = y0 ∀t ∈ [t0 − δ, t0 + δ] (6) .. . ϕ(n−1) (t0 ) = yn−1 . Teorema di Cauchy per le equazioni di ordine n. Sia dato il problema di Cauchy (5). Sia f continua in I × D, e siano ∂f (t, x0 , . . . , xn−1 ), . . ., ∂x∂f (t, x0 , . . . , xn−1 ) continue in un intorno di (t0 , y0 , ·, yn−1 ). ∂x0 n−1 Allora ∃δ > 0 ed esiste una soluzione del problema di Cauchy, cioè una funzione ϕ(t) definita e derivabile n volte su [t0 − δ, t0 + δ] ⊆ I tale che: ϕ(n) = f (t, ϕ, ϕ0 , . . . , ϕ(n−1) ), ϕ(t0 ) = y0 .. . ∀t ∈ [t0 − δ, t0 + δ] (7) ϕ(n−1) (t0 ) = yn−1 . La funzione ϕ(t) è l’unica soluzione che passa per (t0 , y0 , . . . , yn−1 ), nel senso che ogni altra soluzione che passa per quel punto coincide con ϕ(t) su tutto l’intervallo [t0 − δ, t0 + δ]. 3 Alcuni casi particolari. Formuliamo nuovamente il Teorema di Cauchy per alcuni tipi particolari di equazioni del primo ordine. Teorema di Cauchy per le equazioni a variabili separabili. Sia dato 0 y = a(t)g(y) y(t0 ) = y0 Siano a(t) continua su un intervallo I contenente t0 , g(y) continua su un intervallo D contenente y0 . Sia inoltre g(y) derivabile con continuità in un intorno di y0 . Allora esiste δ > 0 ed esiste ed è unica la soluzione del problema di Cauchy assegnato, definita sull’intervallo [t0 − δ, t0 + δ]. Dimostrazione. La funzione f (t, y) = a(t)g(y) è continua su II × D perché è il prodotto di due funzioni continua di una sola variabile. Inoltre ∂f (t, y) = ∂y a(t)g 0 (t) è continua in un intorno di (t0 , y0 ). Sono quindi verificate le ipotesi del Teorema di esistenza e unicità enunciato in precedenza. Teorema di Cauchy per le equazioni lineari. Sia dato 0 y = a(t)y + b(t) y(t0 ) = y0 Siano a(t) e b(t) continue su un intervallo I contenente t0 Allora esiste δ > 0 ed esiste ed è unica la soluzione del problema di Cauchy assegnato, definita sull’intervallo [t0 − δ, t0 + δ]. Dimostrazione. La funzione f (t, y) = a(t)y + b(t) è continua su I. Inoltre ∂f (t, y) = a(t) che è continua per ipotesi. Sono quindi verificate le ipotesi del ∂y Teorema di esistenza e unicità enunciato in precedenza. Osservazione. In effetti si può dimostrare che tutte le soluzioni delle equazioni lineari sono globali, cioè sono definite su tutto l’intervallo I in cui a e b sono continue. Nel caso delle equazioni del primo ordine, questo risultato si vede direttamente dal calcolo delle soluzioni stesse. Un’equazione differenziale lineare di ordine n è un’equazione del tipo y (n) + an−1 (t)y (n−1) + . . . + a1 (t)y 0 + a0 (t)x = b(t). Formulato un teorema di Cauchy (5) per queste equazioni, basta che tutte le funzioni a0 (t), . . . , an−1 (t) siano continue su uno stesso intervallo I perché siano verificate le ipotesi del teorema di Cauchy, e cioè sia garantita l’esistenza e l’unicità delle soluzioni. Si può anche dimostrare che tutte le soluzioni sono globali. Per ulteriori risultati e per una dimostrazione dei Teoremi qui enunciati vedere per esempio: N. Fusco, P. Marcellini, C. Sbordone, Analisi Matematica due, Liguori, Napoli, 1996 4
Documenti analoghi
Equazioni differenziali ordinarie Alcuni aspetti del problema di Cauchy
 y cos ydx = cos xdx ⇒ sin y = sin x + c.
Poichè dev’essere y(0) = π2 , allora 1 = sin π2 = c, per cui sin y = sin x + 1. Se allora ci fosse una
soluzione in ]0, π[, avremmo che sin y > 1.
L’esiste...
y cos ydx = cos xdx ⇒ sin y = sin x + c.
Poichè dev’essere y(0) = π2 , allora 1 = sin π2 = c, per cui sin y = sin x + 1. Se allora ci fosse una
soluzione in ]0, π[, avremmo che sin y > 1.
L’esiste...
Equazioni differenziali del primo ordine
 Per cercare di determinare la soluzione, operiamo nel seguente modo: osserviamo, prima di tutto,
che se k(y0 ) = 0 la funzione costante y(x) = y0 è una (quindi l’unica) soluzione locale.
Se invece...
Per cercare di determinare la soluzione, operiamo nel seguente modo: osserviamo, prima di tutto,
che se k(y0 ) = 0 la funzione costante y(x) = y0 è una (quindi l’unica) soluzione locale.
Se invece...
Il problema di Cauchy
 |g 0 (x)| ≤ K per ogni x ∈ Σ allora g è lipschitziana in Σ perche
|g (x1 ) − g (x2 )| = |g 0 (b
x ) (x1 − x2 )| ≤ K |x1 − x2 | .
|g 0 (x)| ≤ K per ogni x ∈ Σ allora g è lipschitziana in Σ perche
|g (x1 ) − g (x2 )| = |g 0 (b
x ) (x1 − x2 )| ≤ K |x1 − x2 | .
1 Richiami di teoria sui problemi di Cauchy
 dove w ∈ C 1 (I) è una funzione arbitraria. Si noti che il LTE è esattamente
L[y(tn ); h]. Se supponiamo che w sia sufficientemente regolare e sviluppiamo
in serie di Taylor w(t − jh) e w 0 (t − ...
dove w ∈ C 1 (I) è una funzione arbitraria. Si noti che il LTE è esattamente
L[y(tn ); h]. Se supponiamo che w sia sufficientemente regolare e sviluppiamo
in serie di Taylor w(t − jh) e w 0 (t − ...