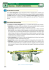PROPOSIZIONI 19 - 22 DI CONOIDI E SFEROIDI

PROPOSIZIONI 19 - 22
DI CONOIDI E SFEROIDI
“La Matematica Greca è permanente, molto più permanente perfino della letteratura greca.
Archimede sarà ricordato quando Eschilo sarà ormai dimenticato, perché le lingue
muoiono ma le idee matematiche no”.
G. H. Hardy (Apologia di un matematico)
Nella Proposizione 21 Archimede giunge a dimostrare che l’area di un conoide rettangolo,
solido ottenuto dalla rotazione completa di un segmento parabolico attorno all’asse della
parabola stessa, è pari ai 3/2 del volume del cono inscritto in esso. Analizziamo, per
meglio comprendere la dimostrazione di tale proposizione, le due proposizioni che la
precedono.
Proposizione 19
Dato un segmento di uno qualunque dei due conoidi (retto o ottusangolo), ottenuto
segando con un piano perpendicolare all’asse, ovvero dato un segmento di uno
qualunque dei due sferoidi (allungato o appiattito), non maggiore della metà dello
(intero) sferoide, similmente ottenuto segando (la figura), è possibile inscrivere (nel
conoide o nello sferoide) una figura solida, e circoscriverne un’altra, composta da
cilindri aventi uguale altezza, in modo che la figura circoscritta superi quella
inscritta per meno di qualunque grandezza solida prefissata.
Ricordiamo che un conoide rettangolo è il solido ottenuto dalla rotazione completa di una
parabola attorno al suo asse e il conoide ottusangolo è il solido ottenuto dalla rotazione
completa di un’iperbole attorno al suo asse trasverso; uno sferoide è invece il solido
ottenuto dalla rotazione completa di un’ellisse attorno al suo asse minore (sferoide
appiattito) o al suo asse maggiore (sferoide allungato). Occupiamoci, in questo contesto,
del conoide rettangolo.
Si inscriva e si circoscriva, dice Archimede, al conoide rettangolo ABC una figura solida
composta da cilindri aventi uguale altezza, il cui asse coincida con quello BD del
segmento parabolico, ottenuta segando la figura con piani perpendicolari all’asse e posti
ad egual distanza l’uno dall’altro.
Con riferimento alla figura si intersechi l’asse BD del conoide rettangolo con dei piani ad
esso perpendicolari e condotti dai punti E, O, Q , P, … , R, equidistanti gli uni dagli altri; le
sezioni ottenute saranno dei cerchi. Si considerino allora i cilindri, circoscritti e inscritti al
conoide rettangolo, aventi per altezze DE,EO,…RB e raggi di base dati dai segmenti
AD,…..,KP, HR intercettati dal conoide rettangolo su tali piani.
Risulta allora che il cilindro componente il solido inscritto è equivalente al cilindro
componente il solido circoscritto ad esso immediatamente sovrastante, avendo i due solidi
base e altezza congruenti per costruzione. Si prenda ad esempio il cilindro inscritto e
quello circoscritto ad esso sovrastante, aventi base comune di centro E e altezze
rispettivamente DE ed EO; oppure il cilindro inscritto e quello circoscritto ad esso
immediatamente sovrastante, aventi base comune di centro O e altezze rispettivamente
EO e OQ. Procedendo in questo modo si giunge all’ultima coppia di cilindri equivalenti: il
cilindro inscritto avente raggio di base KP e altezza PR e quello circoscritto ad esso
sovrastante, avente raggio di base HR=KP e altezza RB.
Risulta quindi che ciascuno dei cilindri circoscritti ha un equivalente cilindro inscritto,
eccetto che il cilindro circoscritto avente base coincidente con la base del solido, ovvero il
cerchio di centro D, raggio AD, e altezza DE, essendo per costruzione sprovvisto di un
equivalente cilindro inscritto immediatamente sottostante ad esso.
Se si indica con Q il volume del solido inscritto nel conoide rettangolo (somma dei volumi
dei cilindri inscritti così costruiti) e con P il volume del solido circoscritto al conoide
rettangolo (somma dei volumi dei cilindri circoscritti così costruiti), risulta P – Q = I , dove I
è il cilindro circoscritto avente per base il cerchio di raggio AD di base del conoide stesso e
per altezza DE.
L’asse del solido BD può essere diviso con un numero, scelto a piacere e molto grande, di
piani su cui giacciono le basi dei cilindri costituenti le figure P e Q, in modo che le altezze
dei cilindri DE = EO = OQ = … = RB siano molto piccole; si giungerà ad un cero punto ad
un solido residuo di volume I, molto piccolo, minore di qualsiasi altro volume prefissato
(qui Archimede usa, come ha fatto in diverse dimostrazioni, la Proposizione I del Libro X
degli Elementi di Euclide).
Proposizione 20
Dato un segmento di uno qualunque dei due conoidi (retto o ottusangolo), staccato
con un piano non perpendicolare all’asse, o (dato un segmento) di uno qualunque
dei due sferoidi (allungato o appiattito), non maggiore della metà dello (intero)
sferoide, similmente staccato (con un piano non perpendicolare all’asse), è
possibile inscrivere nel segmento una figura solida e circoscriverne un’altra,
formata da tronchi di cilindro aventi uguale altezza, in modo che la figura
circoscritta superi quella inscritta per meno di qualunque grandezza solida data.
In questa proposizione Archimede estende i ragionamenti fatti nella proposizione
precedente anche nel caso in cui la figura inscritta e quella circoscritta si ottengano
conducendo dei piani non perpendicolari all’asse.
Proposizione 21
Premesso queste cose, dimostreremo ciò che sulle figure (conoidi e sferoidi) ci
eravamo proposto.
Ogni segmento di conoide rettangolo ottenuto (tagliando) con un piano
perpendicolare all’asse è una volta e mezzo il cono avente la stessa base del
segmento e (lo stesso) asse.
Dato un conoide rettangolo, con asse normale al
piano su cui giace la base, Archimede vuole
dimostrare che il suo volume è pari ai 3/2 del
cono in esso inscritto, che quindi ha la stessa
base del conoide e la stessa altezza.
Si consideri il segmento di conoide rettangolo S
e si sezioni questo con un piano normale alla
base tale che l’asse del solido giaccia tutto sul
detto piano. Sia ABC la parabola giacente sul
piano di rotazione individuato, AC il diametro di
base e BD l’asse, tale che B sia il vertice del
conoide e D il centro della circonferenza di base.
Si consideri il cilindro circoscritto al conoide,
avente la base coincidente con la base del
conoide stesso, e quindi data dal cerchio di
diametro AC, e altezza pari a BD.
Si consideri infine il cono il cui volume X sia pari
a 3/2 del volume del cono inscritto nel conoide,
cioè del cono la cui base è data dal cerchio di
diametro AC e la cui altezza è pari all’asse BD.
Il volume X di un tale cono è la metà del volume
del cilindro circoscritto al conoide. Infatti,
ricordando che il volume di un cono è pari a 1/3
del volume del cilindro ad esso circoscritto,
risulta che:
(
)
“Dico che il segmento del conoide è uguale a X. Infatti se non fosse uguale, sarebbe
maggiore o minore”
Archimede dimostra che il volume del conoide e quello del cono X sono uguali, usando il
metodo di esaustione.
A tal fine, dice Archimede, si inscriva nel conoide una figura Q composta da cilindri aventi
uguale altezza e si circoscriva una figura P composta anch’essa da cilindri aventi altezza
uguale a quelli inscritti, le cui basi stanno su dei piani equidistanti tra loro e perpendicolari
all’asse BD, come illustrato nella Proposizione 19. Con riferimento alla figura, i cilindri che
costituiscono i solidi inscritti e circoscritti, sono rappresentati, in sezione, dai rettangoli con
le basi parallele ad AC ed altezze date da DE, EF,…IB. Si ricordino le caratteristiche di tali
solidi P e Q illustrate nell’analisi della Proposizione 19 e, in particolare, si osservi che se si
indica con n il numero delle parti congruenti in cui si divide l’asse BD, i cilindri componenti
la figura inscritta sono n–1 mentre quelli componenti quella circoscritta sono n.
Si consideri inoltre il cilindro circoscritto al conoide, avente raggio di base AD e altezza
BD; i piani perpendicolari all’asse tracciati in precedenza per costruire le figure P e Q,
divideranno tale cilindro in un numero di cilindri uguale a quello dei cilindri della figura P
circoscritta, cioè n, ciascuno di volume uguale al maggiore dei cilindri di P, cioè a quello
che ha base di raggio AD e altezza DE.
- Si supponga S > X
Potendo dividere l’asse BD in un numero n grande a piacere di parti, si giungerà ad un
certo punto ad un solido residuo di volume I=P-Q, molto piccolo, minore di qualsiasi altro
volume prefissato (qui Archimede usa la Proposizione I del Libro X degli Elementi di
Euclide e la Proposizione 19) e quindi minore della supposta differenza tra S e X:
P–Q<S–X
Essendo, per costruzione, il volume P della figura circoscritta al conoide maggiore del
volume S del conoide, ossia P > S, perché la disuguaglianza sopra scritta sia verificata
deve necessariamente essere Q > X.
Si considerino ora tre tipi di cilindri; siano:
Ci i cilindri componenti la figura inscritta Q,
C’i i cilindri componenti la figura circoscritta P
C”i i cilindri componenti il cilindro circoscritto al conoide.
Si osservi “che dei cilindri, poi, dei quali è composta la figura inscritta, il maggiore sia
quello avente per base il cerchio di diametro KL e per asse DE, mentre il minore sia
quello avente per base il cerchio di diametro ST e per asse la HI” (cit da Opere di
Archimede, A. Frajese)
Essendo ABC una parabola e A e K due suoi
punti (per una proprietà dimostrata da Euclide
nei suoi Elementi) si ha:
.
Si considerino i triangoli simili ABD e OBE
(hanno entrambi un angolo retto e gli angoli
acuti adiacenti alle basi AD e OE congruenti in
quanto corrispondenti, essendo le rette AD e
OE parallele). Si può perciò scrivere:
Per cui risulta:
.
Si calcoli ora il rapporto tra i volumi dei cilindri
C”1 e C1, aventi asse comune DE e base
giacente sul medesimo piano.
Analogamente essendo A e N due punti della parabola ABC, si ha
Se si considerano i triangoli simili ABD e PBF, si può scrivere:
Per cui risulta:
.
Si calcoli ora il rapporto tra i volumi dei cilindri C2’’ e C2, aventi asse comune FE e base
giacente sul medesimo piano (e con AD=QE).
Si proceda similmente per tutti i cilindri inscritti fino a giungere all’ultimo cilindro inscritto,
per cui vale la relazione:
, dove G è il punto d’intersezione di AB con
TS.
Si tenga presente che per costruzione C1’’ = C2’’ = … = Cn’’; per cui il volume di ognuno
dei cilindri in cui è diviso il cilindro circoscritto al conoide lo indicheremo semplicemente
con C’’. Si può allora scrivere:
………………..
e segue che
Ma
e
è il volume del cilindro circoscritto al conoide rettangolo:
è il volume Q del solido inscritto nel conoide rettangolo, ossia:
Consideriamo il Lemma 1 della Proposizione 1 di quest’opera (e dimostrato nella
proposizione 11 di Spirali): Se si hanno grandezze in progressione crescente e altrettante
grandezze tutte uguali tra loro e uguali alla maggiore delle grandezze in progressione
allora sono verificate le seguenti relazioni:
nAn < 2 (A1+ A2 + … +An)
nAn > 2 (A1+ A2 + … +An-1)
Ci troviamo nelle ipotesi di questo Lemma: abbiamo delle grandezze in progressione
crescente IG,…, FP, EO=An-1, (AD=An) e delle grandezze tutte uguali AD, AD,… ed uguali
alla maggiore delle grandezze in progressione; per cui:
da cui si deduce che
contrariamente a quanto supposto all’inizio di questa dimostrazione.
Quindi non può essere S>X
- Si supponga S < X
Potendo dividere l’asse BD in un numero n grande a piacere di parti, si giungerà ad un
cero punto ad un solido residuo di volume I=P-Q, molto piccolo, minore di qualsiasi altro
volume prefissato (qui Archimede usa la Proposizione I del Libro X degli Elementi di
Euclide e la Proposizione 19) e quindi minore della supposta differenza tra X e S:
P–Q<X–S
Essendo, per costruzione, il volume Q della figura inscritta al conoide minore del volume S
del conoide, ossia Q<S, perché la disuguaglianza sopra scritta sia verificata deve
necessariamente essere P<X. Spieghiamolo :
{
Si considerino come prima tre tipi di cilindri; siano:
Ci i cilindri componenti la figura inscritta Q,
C’i i cilindri componenti la figura circoscritta P
C”i i cilindri componenti il cilindro circoscritto al conoide.
Si osservi “che dei cilindri, dei quali è composta la figura circoscritta, il maggiore sia quello
avente per base il cerchio di diametro AC e per asse la retta DE, mentre il minore sia
quello avente per base il cerchio di diametro ST e per asse la BI” (cit da Opere di
Archimede, A. Frajese)
Per costruzione C1’=C1’’, trattandosi di cilindri aventi
base di diametro AC e altezza ED; per cui è
sicuramente vera la proporzione:
Essendo ABC una parabola e A e K due suoi punti
si ha:
.
Si considerino i triangoli simili ABD e OBE (hanno
entrambi un angolo retto e gli angoli acuti adiacenti
alle basi AD e OE congruenti in quanto
corrispondenti, essendo le rette AD e OE parallele).
Si può perciò scrivere:
Per cui risulta:
.
Si calcoli ora il rapporto tra i volumi dei cilindri C”2 e
C’2, aventi asse comune EF e base giacente sul medesimo piano (con QE=AD).
Analogamente, considerando i punti A e N della parabola ABC, si ha
Se si considerano i triangoli simili ABD e PBF, si può scrivere:
Per cui risulta:
.
Si calcoli ora il rapporto tra i volumi dei cilindri C3’’ e C3, aventi asse comune e congruente
a FE e base giacente sul medesimo piano.
Si proceda similmente per tutti i cilindri circoscritti fino a giungere all’ultimo cilindro
circoscritto, per cui vale la relazione:
, essendo G il punto d’intersezione
tra AB e TI.
Si tenga presente che per costruzione C1’’ = C2’’ = … = Cn’’, per cui il volume di ognuno
dei cilindri in cui è diviso il cilindro circoscritto al conoide lo indicheremo semplicemente
con C’’. Si può allora scrivere:
………………..
e segue che
Ma
è il volume del cilindro circoscritto al conoide rettangolo:
e
è il volume P del solido circoscritto al conoide rettangolo, ossia:
Siamo nuovamente nelle ipotesi del Lemma 1 della Proposizione 1 di quest’opera: Se si
hanno grandezze in progressione crescente e altrettante grandezze tutte uguali tra loro e
uguali alla maggiore delle grandezze in progressione allora sono verificate le seguenti
relazioni:
nAn < 2 (A1+ A2 + … +An)
nAn > 2 (A1+ A2 + … +An-1)
In questo caso abbiamo delle grandezze in progressione crescente IG,…,FP,EO, DA=An
e delle grandezze tutte uguali AD, AD,… ed uguali alla maggiore delle grandezze in
progressione; per cui:
da cui si deduce che
contrariamente a quanto supposto in precedenza.
Quindi non può essere neppure S<X
Non potendo essere S<X e neppure S>X, deve necessariamente essere S=X, ossia
Proposizione 22
Anche se il segmento di conoide rettangolo viene ottenuto (tagliando) con un piano
non perpendicolare all’asse, similmente esso sarà uguale ad una volta e mezza il
segmento di cono avente la stessa base e lo stesso asse.
Quanto dimostrato nella proposizione 21 per i segmenti di conoide rettangolo con base
normale all’asse si può estendere a qualsiasi conoide rettangolo non avente base normale
all’asse. Ciò viene dimostrato da Archimede, in modo analogo a quanto fatto nella
Proposizione 21, sempre utilizzando il metodo di esaustione.